Retail Cost Optimization using PythonTo maximize sales and profit, it is important to determine the best-selling cost for goods and services. This tutorial is for those who want to understand how to utilize machine learning to optimize retail costs. We'll guide you through the Python Retail Cost Optimisation with Machine Learning job in this tutorial. Retail Cost Optimization: Finding the ideal equilibrium between the cost you charge for your items and the number of units you can market at that cost is the key to optimizing retail pricing. The final goal is to set a pricing that would enable you to profit the most while luring enough clients to purchase your goods. Finding the optimum cost that maximizes your sales and profits while maintaining customer satisfaction includes using information and pricing techniques. Therefore, you need information on product pricing, service costs, and everything else that influences product costs to complete the retail cost optimization process. For this purpose, we have located the perfect dataset. In the following part, we'll walk you through retail cost optimization using machine learning. Retail Cost datasetImporting the appropriate Python libraries will allow us to begin the Retail Cost Optimisation job. Pricing is extremely important in the fiercely competitive retail sector to draw customers and increase profitability. Pricing decisions are complicated and affected by several variables, including market demand, competition, targeted profit margins, and cost of goods sold (COGS). In order to maximize sales while retaining profitability, businesses must optimize their pricing methods. Here is a piece of information that was submitted to Kaggle focused on the optimization of retail costs. All the information's characteristics are listed below:
Main table (for reference only): Rest of the fields are discussed below:
Utilizing this information will enable you to create an information-driven pricing optimization plan that maximizes revenue. Continuation of Main Table (for reference only): Reading the DataSource Code Snippet Output: product_id1 product_category_name1 month_year qty total_cost1 \
1 sofa1 sofa_bath_table 11-16-2118 1 46.26
1 sofa1 sofa_bath_table 11-16-2118 4 148.86
2 sofa1 sofa_bath_table 11-18-2118 6 286.81
4 sofa1 sofa_bath_table 11-18-2118 4 184.81
4 sofa1 sofa_bath_table 11-12-2118 2 21.21
freight_cost unit_cost product_name_lenght product_description_lenght \. . .
1 16.111111 46.26 42 161
1 12.244444 46.26 42 161
2 14.841111 46.26 42 161
4 14.288611 46.26 42 161
4 16.111111 46.26 42 161
product_photos_qty . . . comp_1 ps1 fp1 comp_2 ps2 \. . .
1 2 ... 82.2 4.2 16.111828 216.111111 4.4
1 2 ... 82.2 4.2 14.862216 212.111111 4.4
2 2 ... 82.2 4.2 14.224844 216.111111 4.4
4 2 ... 82.2 4.2 14.666868 122.612814 4.4
4 2 ... 82.2 4.2 18.886622 164.428811 4.4
fp2 comp_4 ps4 fp4 lag_cost
1 8.861111 46.26 4.1 16.111111 46.21
1 21.422111 46.26 4.1 12.244444 46.26
2 22.126242 46.26 4.1 14.841111 46.26
4 12.412886 46.26 4.1 14.288611 46.26
4 24.424688 46.26 4.1 16.111111 46.26
[6 rows x 41 cols]
Before continuing, let's check to see if the information contains null values: Source Code Snippet Output: product_id1 1 product_category_name1 1 month_year 1 qty 1 total_cost1 1 freight_cost 1 unit_cost 1 product_name_lenght 1 product_description_lenght 1 product_photos_qty 1 product_weight_g 1 product_score 1 customers 1 weekday_1 1 weekend 1 holiday 1 month 1 year 1 s 1 volume 1 comp_1 1 ps1 1 fp1 1 comp_2 1 ps2 1 fp2 1 comp_4 1 ps4 1 fp4 1 lag_cost 1 dtype: int64 Let's now examine the information's descriptive statistics: Source Code Snippet Output: qty total_cost1 freight_cost unit_cost \
count 686.111111 686.111111 686.111111 686.111111
mean 14.426662 1422.818828 21.682281 116.426811
std 16.444421 1811.124111 11.181818 86.182282
min 1.111111 12.211111 1.111111 12.211111
26% 4.111111 444.811111 14.861212 64.211111
61% 11.111111 818.821111 18.618482 82.211111
86% 18.111111 1888.422611 22.814668 122.221111
max 122.111111 12126.111111 82.861111 464.111111
product_name_lenght product_description_lenght product_photos_qty \
count 686.111111 686.111111 686.111111
mean 48.821414 868.422418 1.224184
std 2.421816 666.216116 1.421484
min 22.111111 111.111111 1.111111
26% 41.111111 442.111111 1.111111
61% 61.111111 611.111111 1.611111
86% 68.111111 214.111111 2.111111
max 61.111111 4116.111111 8.111111
product_weight_g product_score customers ... comp_1 \
count 686.111111 686.111111 686.111111 ... 686.111111
mean 1848.428621 4.186614 81.128118 ... 82.462164
std 2284.818484 1.242121 62.166661 ... 48.244468
min 111.111111 4.411111 1.111111 ... 12.211111
26% 448.111111 4.211111 44.111111 ... 42.211111
61% 261.111111 4.111111 62.111111 ... 62.211111
86% 1861.111111 4.211111 116.111111 ... 114.266642
max 2861.111111 4.611111 442.111111 ... 442.211111
ps1 fp1 comp_2 ps2 fp2 comp_4 \
count 686.111111 686.111111 686.111111 686.111111 686.111111 686.111111
mean 4.162468 18.628611 22.241182 4.124621 18.621644 84.182642
std 1.121662 2.416648 42.481262 1.218182 6.424184 48.846882
min 4.811111 1.126442 12.211111 4.411111 4.411111 12.211111
26% 4.111111 14.826422 64.211111 4.111111 14.486111 64.886814
61% 4.211111 16.618284 82.221111 4.211111 16.811866 62.211111
86% 4.211111 12.842611 118.888882 4.211111 21.666248 22.221111
max 4.611111 68.241111 442.211111 4.411111 68.241111 266.611111
ps4 fp4 lag_cost
count 686.111111 686.111111 686.111111
mean 4.112181 18.266118 118.422684
std 1.244222 6.644266 86.284668
min 4.611111 8.681111 12.861111
26% 4.211111 16.142828 66.668861
61% 4.111111 16.618111 82.211111
86% 4.111111 12.448888 122.221111
max 4.411111 57.231111 364.111111
[8 rows x 29 cols]
Let's now examine how the product costs were distributed: Source Code Snippet Output: 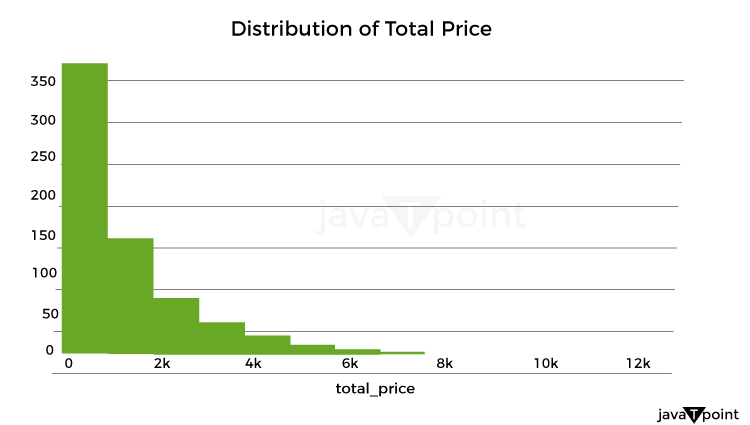 Let's now examine the unit cost distribution using the following plot: Source Code Snippet Output: 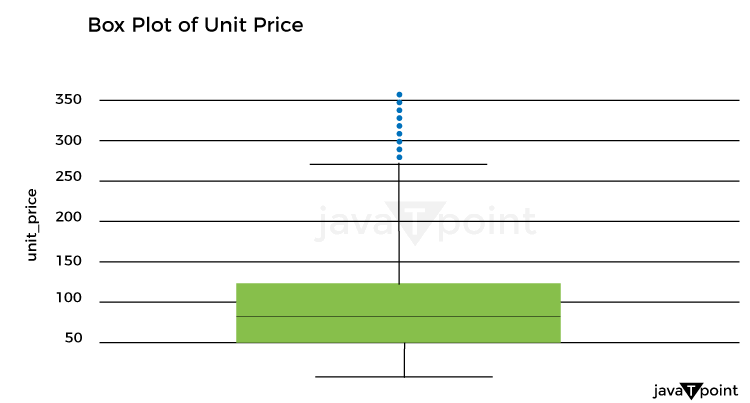 Let's now examine the correlation between quantity and overall pricing: Source Code Snippet Output: 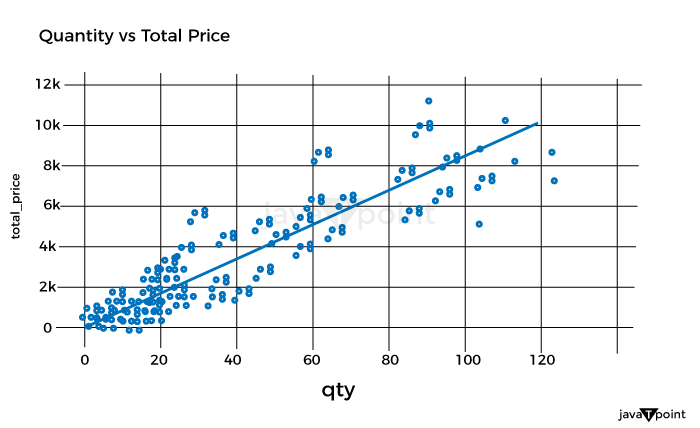 As a result, there is a simple connection between quantity and overall pricing. It implies that the pricing strategy is based on a fixed unit cost, with the quantity times the unit cost multiplied to arrive at the final cost. Let's now examine the average overall pricing for the various product categories: Source Code Snippet Output: 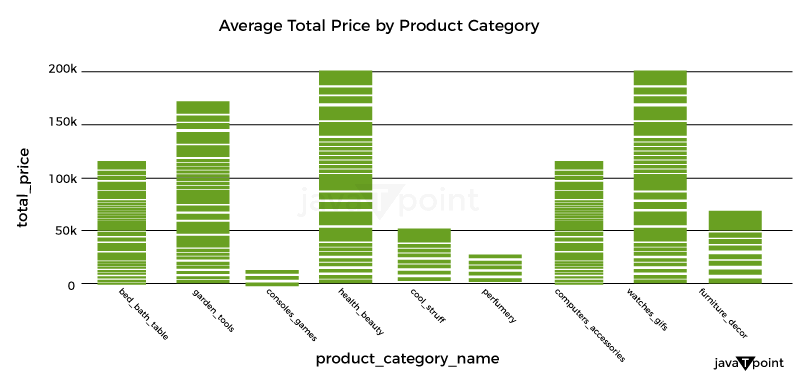 Let's now use a box plot to examine the variation of total costs by weekday_1: Source Code Snippet Output: 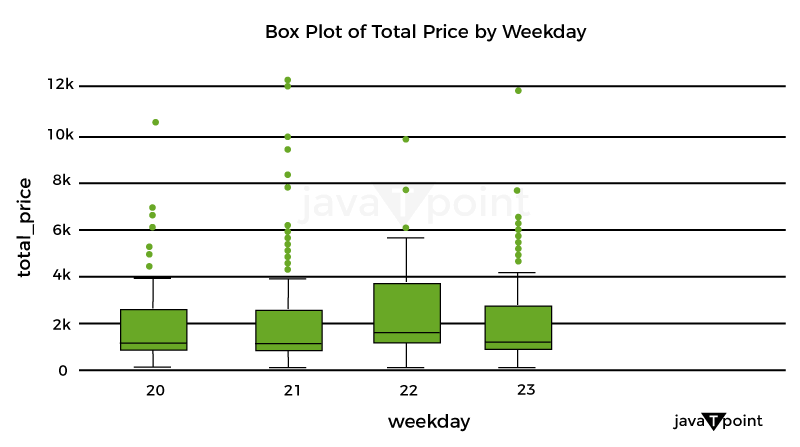 Let's now examine the box plot used to display the breakdown of total costs per holiday: Source Code Snippet Output: 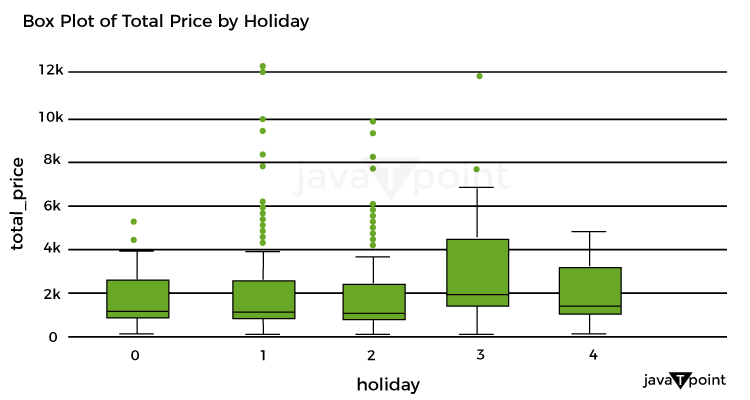 Let's now examine the relationship between the numerical characteristics: Source Code Snippet Output: 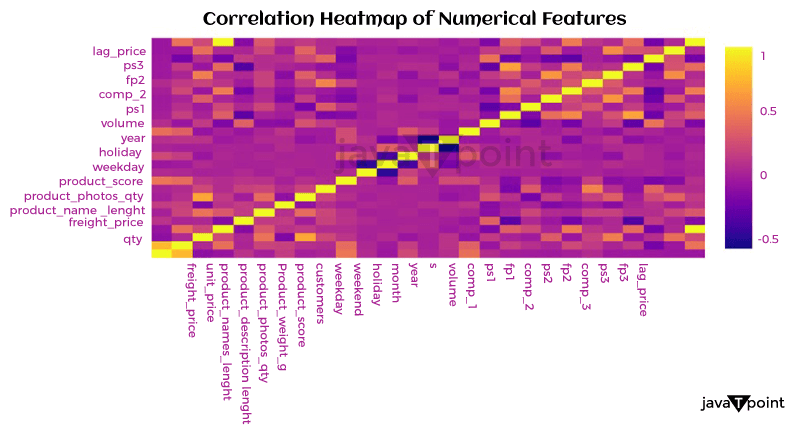 Optimizing retail costs requires a thorough examination of rivals' pricing tactics. According to the retailer's positioning and strategy, monitoring and gauging against rivals' costs can assist in finding possibilities to cost professionally, either by pricing that is below or above the competition. Let's now determine the typical competition cost differential for each product category: Source Code Snippet Output: 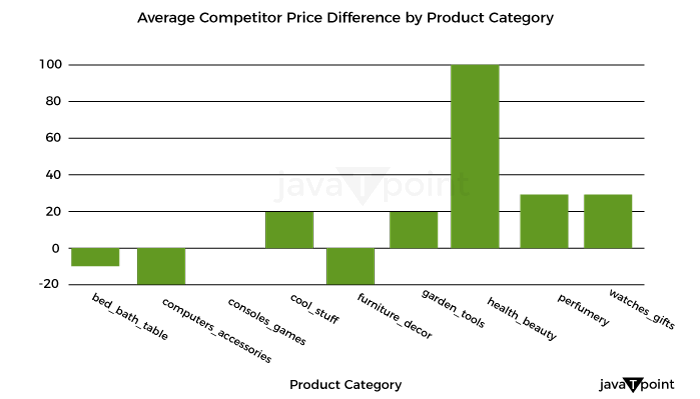 Well known Optimization MethodsTraditional marketers made most of their pricing decisions intuitively, paying little attention to consumer behavior, market trends, the impact of promotions, holidays, or how they affected how sensitively the items responded to cost. Most firms are utilizing big information technology to optimize pricing decisions due to advancements in high computational capabilities that allow an analysis of enormous amounts of information over time. This provides a more competitive cost while ensuring maximum clearance/revenue/margin objectives are met.  It might be difficult to determine the best cost or discount rate for various reasons. One is the intricate design of the pricing approach, which frequently consists of several factors that must be optimized, such as cost lists, reductions, and special offers. Another factor is the need to evaluate new pricing methods more effectively due to the intricacy of demand and profit projections. A technical difficulty in the process is the choice of the optimal modelling and optimization methods. The process for determining costs for maximizing one metric while maintaining the other measurement at a minimum in detail below. It will consider consumer behavior, holidays, competitor pricing, the impact of cannibals, the effectiveness of advancement for costs, and most importantly, how to decide the costs for these factors. For instance, a shop could need to achieve margins above a minimum of 21% while maximizing the sale of winter goods throughout the summer. To help with implementation, I have also given the pertinent codes in several parts. It is usually useful to code as many processes as possible on PySpark to speed up the code for all large information operations. Numerous PySpark libraries are continually being created and enhanced. However, the preprocessing (common computations and aggregations) and generic linear modelling libraries have been fully developed and are quite useful. Since PySpark currently lacks fully tested libraries for optimization that meet the needs of our situation, we will do the initial stages in PySpark and the optimization step in Python. With the appropriate syntax adjustments, the same functionality may be implemented in Python for users who don't have a Spark Setup or for whom the amount of the information is fine. ClusteringThis stage may be applied in one of two ways: 1) to group stores with comparable product adaptability and customer behavior to reduce the number of models and address the issue of information sparsity, or 2) to analyze the information. As a result, each key is modeled in a store cluster rather than for each key in a store. 2) The group of identifiers can guide the model to learn anything about related stores if computing capacity isn't an issue. To determine the clusters based on the information at hand, k-means clustering methods can be utilized. ModellingEmploying a cost elasticity model is typically recommended since the coefficients may be utilized to create the optimization equations and determine if the appropriate characteristics are given the appropriate weight. The amount required in response to a single percent cost shift may be calculated using cost elasticity. The coefficient provides the slope when you plot the volume log upon the cost log. Before fitting the model, you should standardize or normalize the values and take additional pretreatment measures to ensure the information complies with the linear regression assumptions. Depending on the necessity for variable selection, you can start by testing a general linear regression (OLS) before moving on to ridge/lasso models. The coefficients that result from the model provide you with the parameters of the equation once you have finished choosing and tweaking the model. Consequently, your final equation for every single item will be like this: CannibalizationAn established dynamic is cannibalization. It describes the decline in sales (in terms of both units and dollars) of a company's current products due to the launch of a new product or existing comparable items. One frequent illustration is how sales of a product from brand A are absorbed by those of a product from brand B that is similarly cost. When modelling for cost optimization, cannibalization is a fairly noticeable effect that is frequently ignored. According to the theory, incorporating in the model at least the pricing/discount % of the top 5 omnivores of each product can talk a lot about the effect via the coefficients and drive the cost in the appropriate direction during optimization. Optimization Model for Retail Cost with Machine LearningLet's now train a model using machine learning to optimize retail costs. We can train an automated learning framework for this issue, as shown below: Source Code Snippet Output: 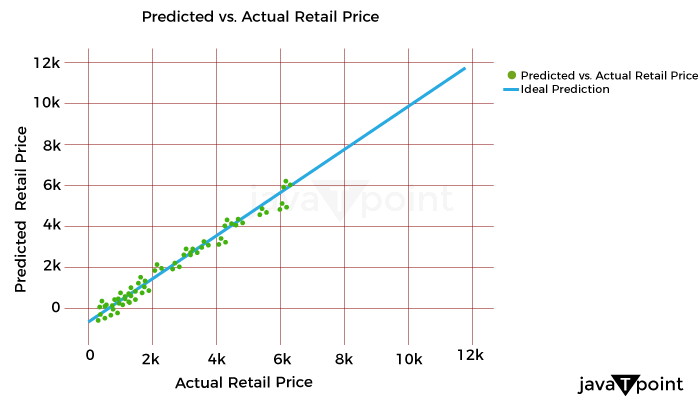 Consolidated Code for Retail Cost Optimization using PythonSo, this is how Python and machine learning can be used to optimize retail pricing. SummaryThe ultimate goal of retail cost optimization is to set a cost that maximizes your profit while drawing in a sizable enough client base to support your business. Finding the optimum cost that maximizes your revenue and sales while maintaining customer satisfaction includes using information and methods for pricing. I hope you enjoyed reading this post on Python-based machine learning for retail pricing optimization. Next TopicFake News Detector using Python |