Python - Logistics Distribution in Statistics

Probability distributions are the cornerstone of statistical analysis, providing a structured way to describe and understand the variability within data. Among these distributions, the logistic distribution stands out as a versatile tool, particularly well-suited for modeling scenarios where outcomes are bounded between two limits. The logistic distribution finds applications in various fields, from predicting binary outcomes to understanding growth rates. In this post, we will investigate the features of the logistic distribution, decipher its complexities, and discover how to use Python to its fullest advantage. After this journey, you will have a firm understanding of how to use logistic distributions and apply them successfully to various statistical and predictive problems.

What are Logistic Distributions?

In statistics, a logistic distribution is a vital probability distribution used in modeling and analyzing various real-world phenomena. This distribution is particularly valuable when dealing with situations where outcomes are constrained within a specific range, often bounded between two values. The logistic distribution's distinctive S-shaped curve makes it an excellent choice for capturing sigmoid-like behavior, which is prevalent in numerous natural and social processes.

Mathematically, the logistic distribution is defined by two key parameters: the location parameter μ (mu) and the scale parameter s (sigma). The location parameter represents the mean of the distribution, indicating where the peak of the curve is centered. The scale parameter determines the spread or variability of the distribution.

A complex but elegant expression gives the probability density function (PDF) of the logistic distribution: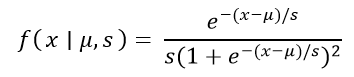

Here, x denotes the random variable, μ denotes the location parameter, and s denotes the scale parameter. Given the distribution's parameters, this function defines the likelihood of observing a particular value x.

Moreover, the cumulative distribution function (CDF) of the logistic distribution is of paramount importance. It takes the form of the sigmoid function, which exhibits an S-shaped curve: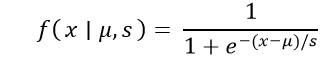

In this equation, F(x) represents the probability that the random variable x is less than or equal to a given value.

The logistic distribution is a versatile tool for understanding and modeling bounded outcomes with sigmoidal tendencies, making it an indispensable asset in statistical analysis and predictive modeling.

Applications of Logistics Distributions in Statistics

With its unique properties and versatility, the logistic distribution finds many applications across various domains in statistics. This distribution's ability to model bounded outcomes and exhibit sigmoid-like behavior makes it an invaluable tool for addressing many real-world scenarios. Here are some notable applications of the logistic distribution in statistics:

Logistic Regression: One of the logistic distribution's most well-known uses is in logistic regression. When attempting to forecast the likelihood of a binary result, this statistical strategy is used for binary classification problems. Logistic regression is built on the cumulative distribution function of the logistic distribution, sometimes called the logistic function or sigmoid function. It is perfect for modeling probabilities of binary outcomes since it converts the linear combination of predictor variables into a probability value between 0 and 1.

Epidemiology and Medical Sciences: Logistic distributions are frequently used to model various medical phenomena, such as the probability of disease occurrence. For instance, logistic distributions can be employed to analyze the likelihood of a patient's medical condition based on risk factors and symptoms. These distributions can also be useful in epidemiology to model disease transmission probabilities and evaluate the effectiveness of interventions.

Market Research and Economics: In market research, logistic distributions are applied to model consumer behaviors and preferences. For example, they can be used to analyze the likelihood of customers purchasing a product based on demographic or behavioral characteristics. In economics, logistic distributions find use in modeling outcomes with limited ranges, such as the probability of an individual defaulting on a loan or the likelihood of a stock price crossing a certain threshold.

Ecology and Biology: Logistic distributions play a role in ecological modeling, particularly in population growth and carrying capacity scenarios. They can describe the growth of species populations up to a certain limit as resources become constrained. Logistic distributions might be used in genetics to model the probability of an organism inheriting a specific genetic trait.

Psychology and Social Sciences: In psychology and social sciences, logistic distributions can help model behaviors that have natural limits. For instance, they can be applied to understand the likelihood of individuals adopting a certain behavior or responding to a particular stimulus. This can aid in predicting trends in human behavior and decision-making.

Quality Control and Manufacturing: Logistic distributions can be utilized in quality control processes to model the probability of a manufactured product meeting certain specifications. This is particularly useful when the outcome is binary, such as pass/fail or acceptable/defective. Logistic distributions help assess the likelihood of a product falling within acceptable quality limits.

In each of these applications, the logistic distribution's ability to capture the bounded and sigmoidal nature of various outcomes proves highly beneficial. By employing this distribution, statisticians and data analysts can gain insights, make predictions, and make informed decisions in various fields.

Properties of Logistic Distribution

1. Symmetry: The logistic distribution exhibits symmetry around its mean μ. The two halves would match perfectly if you fold the curve at its mean. In mathematical terms, for any value x to the left of the mean μ, there is a corresponding value ′x′ to the right of the mean such that μ-x=x′-μ. This property is visually apparent when you look at the distribution's probability density function (PDF) shape, which forms a mirror image on both sides of the mean.
2. S-Shaped Curve: The signature S-shaped curve of the logistic distribution arises from its probability density function (PDF) and cumulative distribution function (CDF). This shape is particularly advantageous when modeling processes that exhibit sigmoid-like behavior, where outcomes initially increase gradually, then steeply, and finally plateau. This behavior is common in various natural and social processes, making the logistic distribution suitable for modeling situations with saturation points or natural limits.
3. Bounded Outcomes: One of the key features of the logistic distribution is its ability to model bounded outcomes. While the distribution approaches its asymptotic bounds of 0 and 1, it never actually touches them. This is valuable for scenarios where outcomes are naturally constrained within a specific range, such as probabilities that range from 0 to 1. The distribution smoothly captures how probabilities or proportions change as they approach their limits.
4. Location and Scale Parameters: The logistic distribution is parameterized by two main parameters: the location parameter μ and the scale parameter s. The location parameter determines the center of the distribution, indicating the mean or peak value. For example, if μ is set to 0, the peak of the distribution will be at 0. The scale parameters control the spread or variability of the distribution. Larger values of s result in wider distributions.
5. Mean and Variance: The logistic distribution's mean (or expected value) is equal to its location parameter μ. This means that the peak of the distribution is centered at μ. The variance of the distribution, denoted as Var(X), is given by S. This demonstrates that the spread of the distribution is influenced by the scale parameter s. Larger values of s result in larger spreads.
6. Cumulative Distribution Function (CDF): The cumulative distribution function (CDF) of the logistic distribution is the logistic function, often denoted as F(x). This function transforms any real number x into a value between 0 and 1, making it suitable for modeling and cumulative probabilities. The sigmoidal shape of the logistic function allows it to gradually approach its asymptotes at 0 and 1 without ever reaching them.
7. Tail Behavior: The tails of the logistic distribution gradually approach but never touch the horizontal axis. This property contrasts distributions with heavier tails, like the Cauchy distribution. The logistic distribution's tails decline asymptotically, which means that the probability of observing extreme values never reaches zero. This is relevant when modeling rare events or outliers.
8. Relationship to Standard Normal Distribution: As the scale parameter s of the logistic distribution increases, its shape becomes more similar to that of the standard normal distribution (mean 0 and variance 1). The logistic distribution approaches the standard normal distribution in that its tails become more similar to the tails of the standard normal distribution.

Python Implementation

Implement the logistic distribution in Python using the scipy.stats library, and then I'll explain the code step by step. First, make sure you have scipy installed; you can install it using pip if you haven't already:

Below given a Basic Python implementation of the logistic distribution:

Output: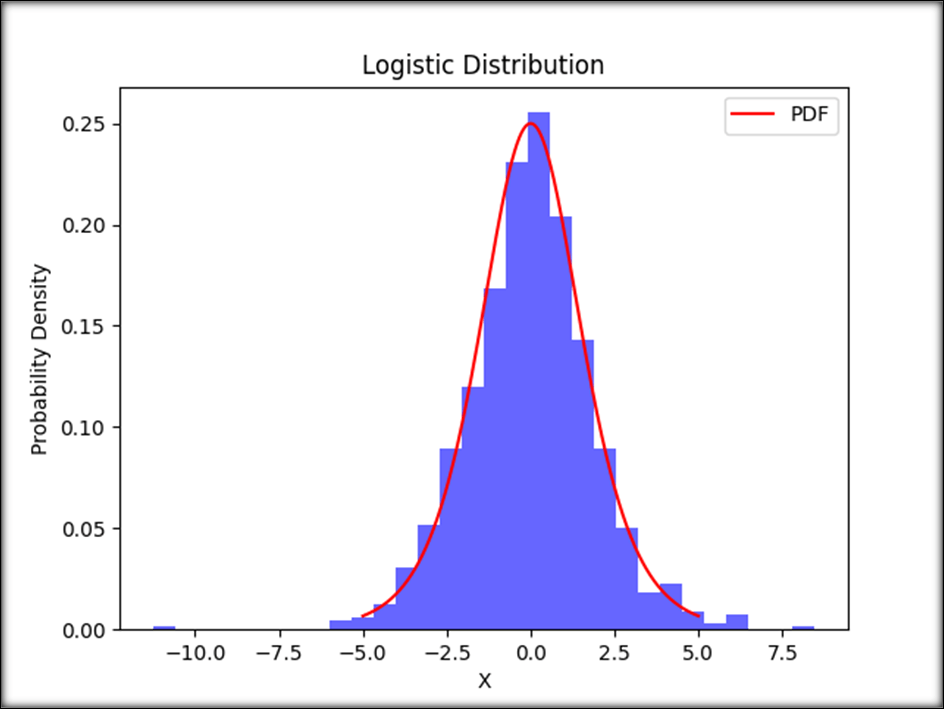

Explanation of the Code:

1. We start by importing the necessary libraries:
   • numpy for numerical operations.
   • pyplot for creating plots.
   • stats.logistic for working with the logistic distribution.
2. We define the parameters for the logistic distribution:
   • mu (mean) is set to 0.
   • s (scale) is set to 1. You can adjust these parameters as needed for your specific application.
3. We generate random samples from the logistic distribution using rvs(). This simulates a dataset following the logistic distribution with the specified parameters.
4. We calculate the mean and variance of the generated data using mean() and logistic.var(), respectively.
5. We create a histogram of the generated samples using hist(). This histogram helps visualize the distribution of the data.
6. We calculate the logistic distribution's probability density function (PDF) for a range of values x using pdf(). This PDF represents the theoretical probability distribution of the logistic distribution with the given parameters.
7. We plot the histogram and the PDF on the same graph using plot(). This allows us to compare the simulated data with the theoretical distribution.
8. We add labels, a title, and a legend to the plot to make it more informative.
9. Finally, we display the plot using show().
10. We print out the calculated mean and variance of the data to see how they compare to the specified parameters.

When you run this code, you'll get a visual representation of the logistic distribution and see how the generated data matches the theoretical distribution. This implementation can be a useful starting point for understanding and working with the logistic distribution in Python.

Conclusion

To sum up, the logistic distribution is a potent and adaptable tool in the statistics toolbox. It is incredibly useful for simulating various actual processes due to its unique characteristics, including symmetry, sigmoidal shape, and the capacity to describe constrained outcomes. This distribution is a key building component in statistical analysis, used for anything from understanding growth rates to forecasting probabilities in logistic regression. With the help of the scipy.stats library's Python version, which we've looked at here, statisticians and data analysts may use the logistic distribution to obtain knowledge, forecast the future, and make defensible judgments in various fields. As you continue to explore the world of statistics and data science, the logistic distribution will remain a reliable tool for capturing and understanding the complex dynamics of many natural and social phenomena. The logistic distribution will continue to be a trustworthy instrument for capturing and comprehending the complex dynamics of many natural and social events as you further your statistics and data science studies.