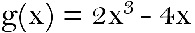Physics Calculations in Python: Introduction to Python Function

Could it be said that you are prepared to move to a higher level with your physical science computations in Python? If this is true, then you want to dominate the python capability. The fact that we like physical science and Python makes us not specialist software engineers; we are typical humans.

I will expect you have proactively made a mathematical computation in Python. It doesn't need to be something insanely muddled. Perhaps it's simply the direction of a shot with no air opposition.

Alright, however, what on God's green earth is a capability?

It's the same as numerical capability. Something like this: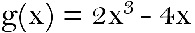

For this number-related function, you can place in whatever worth of x that you like, and it "yields" some worth. A python capability can be very much like this. This could be a python capability. This is what that would resemble.

Function:

• Indeed, this may be the most exhausting python program ever. However, it's an extraordinary spot to begin. Here are a few significant notes:
• The capability needs an extraordinary name. I can utilize "g" for however long there could be no different capabilities or factors named "g".
• You pick the variable info names in the definition (indeed, you want the def part and the colon). For this situation, I'm utilizing "x," yet it may be anything the length of you utilize a similar name in the body of the capability.
• The result is the return() - anything that you put in the enclosure will be the aftereffect of the capability.
• This capability has one info (x) and one result - however, you could have as many data sources and results as you like.

A Projectiles Motion Functions

What about another model that may be useful? I will make a capability that takes the underlying speed vector for an article and the level over the ground. It then returns the "range" - the even distance the article voyages.

Even though I could compute this reach with a logical arrangement, I will do it mathematically, all things being equal. Similarly, as a speedy survey, this is how to figure out how far the item ventures evenly.

• Begin with the underlying position and speed of the item. I can track down the article's energy from the speed and mass.
• Break the movement into modest stretches. What about 0.01 seconds?
• Compute the power of the article. For this situation, being a consistent gravitational force is simply going.
• We can utilize this power and the ongoing energy to track down the new force toward finishing the brief time frame stretch.
• At last, with the energy, I can refresh the place of the article.

Continue to do this circle until the article gets to the "ground", which I will call y1 = 0 meters.

Source Code:

Output: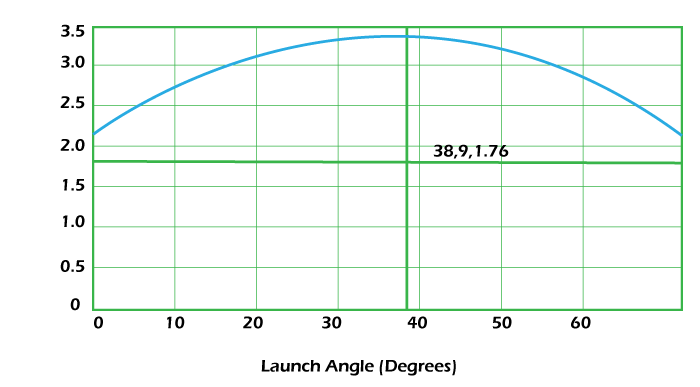

The connection between starting speed, beginning level, and vertical speed can constantly be addressed by the right-calculated triangle with q (as displayed in the graph) is the place where the shot leaves the flat plane (generally the ground). This point is the launch angle.

Presently for remarks:

• In line one, I name the capability xrange(v0,h,m). To start with, I'm almost certain that reach is now a capability in one of the modules stacked in glowscript (indeed, I'm utilizing glowscript). Second, I'm passing three factors into the capability. Look at this, v0 is a vector, and I don't even need to proclaim it as that sort for a moment.
• Line 13 resembles an entire program without anyone else with the circle that does the mathematical computation.
• The circle is until the position is not more prominent than nothing at this point. Since I made the situation as a vector, r.y is the y-part of that position.
• Lines 14, 15, and 16 are all vector conditions. Since p is a vector, the right side is a vector activity. Isn't it unreasonably cool?
• Line 18 returns the last position. This capability has the scalar x-part of the position. However, you could have this as r - perhaps you should attempt that and see what occurs.
• At long last, in lines 20 and 21, I print the result of the capability for a specific arrangement of data sources. This is to ensure the thing is working.
• Presently how about we utilize this thing, will we? I need to find the send-off point that creates the best reach. Here is the code to do that.
• It utilizes that equivalent capability (however, I changed the period from 0.01 to 0.001) previously. Presently for a few additional notes:
• Lines 20-24 are only the underlying circumstances. The mass doesn't change, yet I will involve that only a bit. Likewise, it's simpler to think about the send-off speed regarding greatness and point - yet I convert to a vector before calling the capability.
• Line 22 is the point step. I will call the capability for some underlying send-off point and rehash it for a marginally higher point.
• Lines 26-27 are only for setting up the diagram. Here is your python diagram instructional exercise.
• Lines 29-33 are the circle to run the capability with various send-off points. This incorporates tracking the send-off speed vector (line 30) and plotting stuff (line 32).

Notice that the most extreme reach is at a send-off point of around 36 degrees - and NOT 45 degrees. Recollect that the greatest reach for a shot is 45 degrees when you send off from level ground onto level ground. I sent off the article 1 meter over the floor for this situation.

Indeed, you could utilize a viable, more refined strategy to print out the most extreme reach, yet taking a gander at the diagram works fine as well.