Negative Binomial Discrete Distribution in Statistics in Python

The scipy.stats.nbinom() describes the Negative Binomial Discrete Distribution. It is an instance of the rv_discrete class inherited from the generic methods. It completes the techniques by adding details specific to this distribution.

The Probability Mass Function, which gives the total number of failures for Negative Binomial Discrete Distribution, is given by: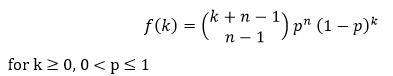

The nbinom contains n and p as the shape parameters where n is the success number, p is the probability of the single success, and 1 - p is the single failure probability.

The mean number of failures to attain success is another popular parameterization of the negative binomial distribution. The mean is related to the likelihood of success: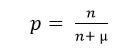

Where µ is the mean

n is the number of successes

We can define the number of successes in terms of the "dispersion", "heterogeneity", or "aggregation" parameter α, which relates the mean µ with the variance σ²,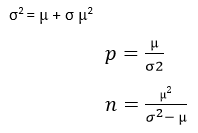

The probability mass function for negative binomial discrete distribution defined above is the standardized form. We use the loc parameters to shift and scale the distribution. The nbinom.pmf(k, n, p, loc) is exactly equal to nbinom.pmf(k - loc, n, p).

Parameters including in the Negative Binomial Discrete Distribution

• x: it refers to the quantiles
• loc: it is used to refer to the location parameter. This parameter is optional, and its default value is 0.
• scale: it refers to the scale parameter. This parameter is optional, and its default value is 1.
• moments: It is composed of different letters ['msvk']:
  • 'm': mean
  • 'v': variance
  • 's': Fisher's skew
  • 'k': Fisher's kurtosis

By default, it is 'mv' (mean and variance)

• Results: It returns the negative binomial discrete random variable.

Python provides the nbinom module under the scipy.stats library, which is used to find the Negative Binomial discrete Distribution.

Importing the nbinom() library in Python

Let's understand the concept of Negative Binomial Discrete Distribution in Statistics with the help of different programs in Python.

Program 1: A program to create Negative Binomial Discrete Random Variable

Code:

Output:

Random Variable : 
 

Explanation:

Using the nbinom() function, we have made a Negative Binomial Discrete Random Variable. Firstly, we imported the nbinom module and assigned two variables, x, and y, with random values. Under the nbinom module, used for the Negative Binomial Discrete Distribution, it has a nbinom() function, which gives the random variable.

Program 2: A program to create Negative Binomial Discrete Random variates and their Probability distribution.

Code:

Output:

Random Variates : 
 [0 0 0 0 0 0 0 1 0 0]

The Probability Distribution : 
 [-1. nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan nan
 nan nan]

Explanation:

We have created the random variates using nbinom.rvs() function and the probability distribution using the lomax.ppf() function using a numpy array with random values.

Program 3: A program to graphically represent the Negative Binomial Discrete Probability distribution.

Code:

Output:

Distribution : 
 [0.         0.08163265 0.16326531 0.24489796 0.32653061 0.40816327
 0.48979592 0.57142857 0.65306122 0.73469388 0.81632653 0.89795918
 0.97959184 1.06122449 1.14285714 1.2244898  1.30612245 1.3877551
 1.46938776 1.55102041 1.63265306 1.71428571 1.79591837 1.87755102
 1.95918367 2.04081633 2.12244898 2.20408163 2.28571429 2.36734694
 2.44897959 2.53061224 2.6122449  2.69387755 2.7755102  2.85714286
 2.93877551 3.02040816 3.10204082 3.18367347 3.26530612 3.34693878
 3.42857143 3.51020408 3.59183673 3.67346939 3.75510204 3.83673469
 3.91836735 4.        ]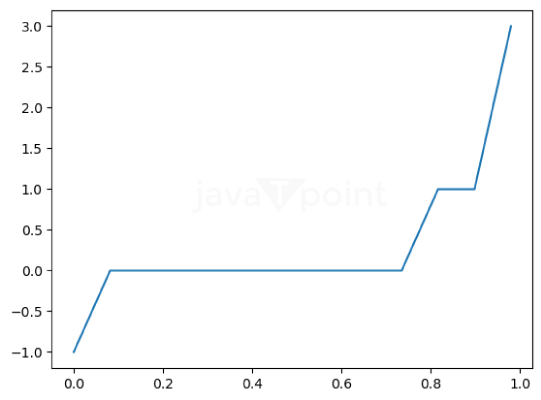

Explanation:

We have printed the distribution using the numpy array, and then, using matplotlib, we have printed a Negative Binomial Discrete Distribution graph using the Percent Point function (.ppf).

Program 4: A program to graphically represent varying positional arguments in the Negative Binomial Discrete Probability Distribution Function.

Code:

Output:

[,
 ]

Explanation:

With the help of linear spacing numbers, we have plotted two different Negative Binomial Discrete Probability Distribution functions using the Percent point function (.ppf) and Probability mass function (.pmf).