Multivariate Linear Regression in Python

"Multivariate Linear Regression" and "Multiple Linear Regression" usually confer the same concept in the context of linear regression modeling. Both terms describe a linear regression version in which you have multiple impartial variables (features) used to expect a single structured variable (target). In different phrases, each phrase means a linear regression version with more than one predictor variable.

Linear regression is a crucial device getting to know the method used for predicting a non-stop purpose variable based totally on one or more unbiased features. When we've got more than one unbiased capability, it is called multivariate linear regression. In this article, we will delve into the area of multivariate linear regression and enforce it in Python.

Understanding Multivariate Linear Regression

Multivariate linear regression extends clean linear regression to a couple of unbiased variables. Instead of getting in reality one feature (X) to predict a goal (Y), we have numerous capabilities (X1, X2, ..., Xn). The purpose stays the same: to locate the exceptional linear dating of a number of the independent variables and the goal variable.

Multivariate linear regression's general formula is:

Y = b₀ + b₁* X₁ + b₂* X₂ +b₃* X₃ + ……………b_n* X_n + ?

The goal variable here is Y and X₁ , X₂ , X₃ , X₄ , …………X_n are the independent variables, b₀ is the intercept, b₁, b₂, b₃, b₄, ………..b_n are the coefficients, and ? represents the error term.

Assumption of Regression Model :

Homoscedasticity: Constant variance of the mistakes must be maintained.
Linearity: The relationship between based and unbiased variables ought to be linear.
Lack of Multicollinearity: It is believed that there is very little multicollinearity within the records.
Multivariate normality: Multiple Regression assumes that the residuals are commonly disbursed.

Input code:

import numpy as np
import matplotlib.pyplot as plt

# Generate the  data
np.random.seed(0)
n_samples = 100
X1 = np.random.rand(n_samples) * 10
X2 = np.random.rand(n_samples) * 5
y = 2 * X1 + 3 * X2 + np.random.rand(n_samples)

# Create a design matrix X by stacking X1 and X2 horizontally
X = np.column_stack((X1, X2))

# Add a column of ones for the intercept term
X = np.column_stack((np.ones(n_samples), X))

# Split the data into training and testing sets
split_ratio = 0.8
split_index = int(n_samples * split_ratio)
X_train, y_train = X[:split_index], y[:split_index]
X_test, y_test = X[split_index:], y[split_index:]

# Calculate the coefficients using the normal equation
coefficients = np.linalg.inv(X_train.T @ X_train) @ X_train.T @ y_train

# Make predictions on the test set
y_pred = X_test @ coefficients

# Calculate Mean Squared Error (MSE)
mse = np.mean((y_test - y_pred) ** 2)

# Calculate R-squared (R^2)
y_mean = np.mean(y_test)
ss_total = np.sum((y_test - y_mean) ** 2)
ss_residual = np.sum((y_test - y_pred) ** 2)
r2 = 1 - (ss_residual / ss_total)

# Print coefficients, MSE, and R-squared
print("Coefficients:", coefficients)
print(f"Mean Squared Error: {mse}")
print(f"R-squared: {r2}")

# Visualize the given data and regression plane
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.scatter(X_test[:, 1], X_test[:, 2], y_test, label='Actual', color='blue')
ax.scatter(X_test[:, 1], X_test[:, 2], y_pred, label='Predicted', color='red', marker='x')
ax.set_xlabel('X1')
ax.set_ylabel('X2')
ax.set_zlabel('y')
ax.legend()
plt.show()

Output:

Coefficients: [0.58539281 1.99996142 2.97306189]
Mean Squared Error: 0.09732995265403607
R-squared: 0.9976043742393531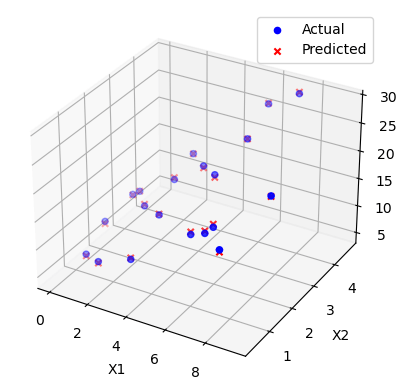

Multivariate Linear Regression in Python

In this code:

We generate artificial facts with two independent variables, X1 and X2, and a goal variable, y.
We create a layout matrix X with the aid of stacking X1 and X2 horizontally and upload a column of ones for the intercept term.
We cut up the facts into training and testing sets.
We calculate the coefficients of the usage of the normal equation for linear regression.
We make predictions at the take a look at set and calculate Mean Squared Error (MSaE) and R-squared (R²)
We visualize the statistics factors and the regression plane using a 3-D scatter plot with matplotlib.

This code performs Multivariate Linear Regression the use of numpy and visualizes the outcomes of the usage of matplotlib.

Understanding the Outcomes

Mean Squared Error (MSE): A decreased MSE indicates a better fit of the model to the facts. It measures the average squared distinction between predicted and actual values.
R-Squared (R²): R-squared measures the share of the variance within the dependent variable (goal) this is predictable from the independent variables. A better value shows a better suit, with 1.0 being an excellent suit.

Next TopicNegative Binomial Discrete Distribution in Statistics in Python

← prev next →