Minimum Swaps to Sort

In this tutorial, we will write the Python program to find the minimum number of swaps required to sort the given list. We have given an array of n distinct elements and we need to find the minimum number of swaps required to sort the array in the increasing order. For example -

Example 1:

Input:

nums = [2, 8, 5, 4]

Output:

1

Explanation:

swap 8 with 4.

Example 2:

Input:

nums = [10, 19, 6, 3, 5]

Output:

2

Explanation:

swap 10 with 3 and swap 19 with 5.

Let's implement the solution of the above problem.

Solution -

Let's understand the visual representation of the above problem. We will have the n nodes and an edge directed from node i to node j if the element at i^th index must be present at the j^th index in the sorted array. Below is the graph for an input.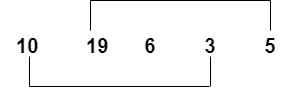

As we can see, there is two swaps are required to sort the array in increasing order. We need to identify the cycle in the given array. Let's understand the following example.

Example -

Output:

Minimum Swap Required:  2

Explanation -

In the above code, first we create a minimum_swaps() function that takes list as an argument. Then we initialize the swaps variable which will track the number of swaps performed. Then we copy the array in arr_copy so that we can perform swaps without making changes in the original array. Then, we sort the copied array to get the expected output. We create a visited array of size n with False to keep track of the visited elements. Then we iterate each element of the array and perform the following step -

a. Check if the current element is already visited or if it is in its correct sorted position (i.e., the current index equals the value of the element minus one).

If true, continue to the next element.

If false, it means we have encountered a new cycle. Initialize a variable cycleSize to 0, which will represent the size of the current cycle.

Enter a loop until we complete the cycle:

i. Mark the current element as visited.

ii. Increment the cycleSize variable.

iii. Update the current element with its correct sorted position.

iv. If the new element is the same as the original element, exit the loop as the cycle is completed.

After exiting the loop, add cycleSize - 1 to the swaps variable. This is because cycleSize - 1 swaps are required to sort a cycle of size cycleSize.

Then we return the value of swaps.

We can solve it without creating a copy of the array and sorting it. We can assume that a given array consists of distinct elements and utilize the cycle detection concept to find the minimum number of swaps required.

Let's understand the following example.

Example -

Output:

2

Explanation -

In the above code, we implement a function called minimum_swaps() that calculates the minimum number of swaps required to sort an array arr in ascending order. It uses a modified version of the selection sort algorithm.

The minimum_swaps() function takes an array arr as input. It initializes two variables: n with the length of the array arr, and swaps as a counter to keep track of the number of swaps performed. Then we use for loop that iterates from 0 to n-1, representing the indices of the elements in the array.

Within the loop, it checks if the current element arr[i] is in its correct sorted position, which would be i + 1 (since the array is expected to contain consecutive numbers starting from 1).

If the element is not in its correct position, it enters a while loop that continues until the element is swapped to its correct position.

Inside the while loop, the code performs the swap operation. It temporarily stores the current element in the variable temp, then swaps the current element with the element at its correct position by accessing arr[temp - 1]. The - 1 is used because array indices start from 0.

After the swap, the counter swaps are incremented by 1.

The while loop continues until the current element is in its correct position, and then the code proceeds to the next iteration of the for loop.

Once the for loop completes, the function returns the total number of swaps performed.

Finally, we pass an array arr with elements [4, 3, 1, 2] and call the minimum_swaps to function with this array as an argument. The result is stored in the variable result.

Finally, the value of the result is printed, which represents the minimum number of swaps required to sort the array. In this case, the output would be 2.