Lomax Distribution in Statistics using Python

The scipy.stats.lomax describes the Lomax continuous random variable. It is an instance of the rv_continuous class inherited from the generic methods. It completes the techniques by adding details specific to this distribution.

The Probability Density Function, which gives the Lomax Distribution, is given by: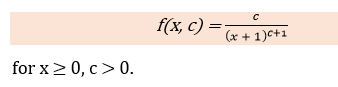

The probability density function for lomax distribution defined is the standardized form. We use the loc and scale parameters to shift and scale the distribution. The shifting of the location does not make it a noncentral distribution. lomax.pdf(x, loc, scale) is exactly equal to lomax.pdf(y, c) / scale with y = (x - loc) / scale. The lomax is a special Pareto case with a loc value = 1.0.

Parameters including in the Lomax Distribution

• q: it is referred to as the probability of the lower and upper tail
• x: it refers to the quantiles
• loc: it is used to refer to the location parameter. This parameter is optional, and its default value is 0.
• scale: it refers to the scale parameter. This parameter is optional, and its default value is 1.
• moments: It is composed of different letters ['msvk']:
  • 'm': mean
  • 'v': variance
  • 's': Fisher's skew
  • 'k': Fisher's kurtosis

By default, it is 'mv' (mean and variance)

• Size: It defines the shape or random variates. It is a tuple of integer data type. It is an optional parameter.
• Results: It returns the Lomax continuous random variable.

Python provides the lomax module under the scipy.stats library, which is used to find the lomax Distribution.

Importing the lomax() library in Python

Let's understand the concept of lomax Distribution in Statistics with the help of different programs with different cases.

Program 1: A program to create Lomax Distribution Random Variable

Code:

Output:

Random Variable : 
 <scipy.stats._distn_infrastructure.rv_continuous_frozen object at 0x000001A778F72D50>

Explanation:

Using the lomax() function, we have made a Lomax distribution random variable. Firstly, we imported the lomax module and assigned two variables, x, and y, with random values. Then using the lomax function, we created the random variable.

Program 2: A program to create Lomax continuous variates and its Probability distribution.

Code:

Output:

Random Variates : 
 4.3263639849502695

The Probability Distribution : 
 [0.00652862 0.00663204 0.00673741 0.00684477 0.00695417 0.00706566
 0.00717927 0.00729506 0.00741308 0.00753338 0.00765599 0.00778099
 0.00790842 0.00803834 0.00817079 0.00830585 0.00844357 0.00858402
 0.00872724 0.00887331 0.0090223  0.00917427 0.00932929 0.00948743
 0.00964876 0.00981337 0.00998132 0.01015269 0.01032758 0.01050605
 0.0106882  0.01087412 0.01106388 0.0112576  0.01145536 0.01165725
 0.01186339 0.01207388 0.01228881 0.01250831 0.01273248 0.01296144
 0.01319531 0.0134342  0.01367825 0.01392759 0.01418234 0.01444265
 0.01470866 0.0149805  0.01525834 0.01554232 0.01583259 0.01612933
 0.01643271 0.01674288 0.01706003 0.01738435 0.01771602 0.01805523
 0.01840218 0.01875709 0.01912015 0.0194916  0.01987164 0.02026053
 0.02065848 0.02106576 0.02148261 0.0219093  0.02234609 0.02279327
 0.02325112 0.02371993 0.02420002 0.02469169 0.02519528 0.02571111
 0.02623954 0.02678092 0.02733562 0.02790403 0.02848653 0.02908353
 0.02969546 0.03032274 0.03096582 0.03162517 0.03230127 0.0329946
 0.03370569 0.03443506 0.03518325 0.03595083 0.03673839 0.03754654
 0.03837588]

Explanation:

We have created the random variates using lomax.rvs() function and the probability distribution using the lomax.pdf() function using a numpy array with random values.

Program 3: A program to graphically represent the Lomax Probability distribution.

Code:

Output:

Distribution : 
 [0.         0.04081633 0.08163265 0.12244898 0.16326531 0.20408163
 0.24489796 0.28571429 0.32653061 0.36734694 0.40816327 0.44897959
 0.48979592 0.53061224 0.57142857 0.6122449  0.65306122 0.69387755
 0.73469388 0.7755102  0.81632653 0.85714286 0.89795918 0.93877551
 0.97959184 1.02040816 1.06122449 1.10204082 1.14285714 1.18367347
 1.2244898  1.26530612 1.30612245 1.34693878 1.3877551  1.42857143
 1.46938776 1.51020408 1.55102041 1.59183673 1.63265306 1.67346939
 1.71428571 1.75510204 1.79591837 1.83673469 1.87755102 1.91836735
 1.95918367 2.        ]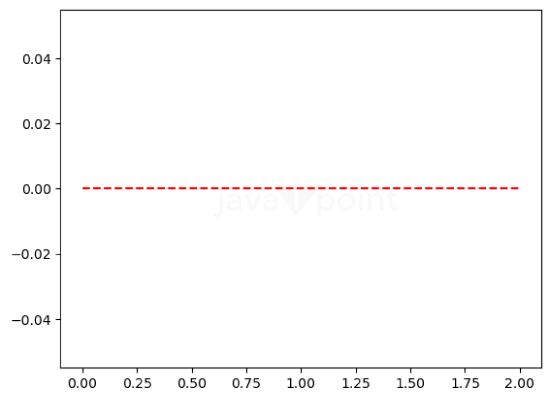

Explanation:

We have printed the distribution using the numpy array, and then using matplotlib, we have printed a graph of the Lomax Distribution using the Probability Density function.

Program 4: A program to graphically represent varying positional arguments in the Lomax Probability Distribution Function.

Code:

Output: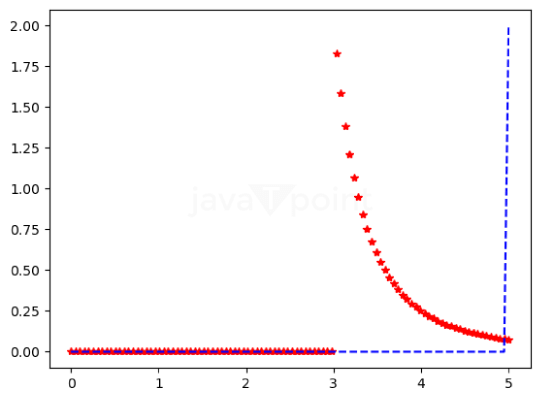

[,
 ]

Explanation:

We made a numpy array with linear, equal spaces, then plotted a graph with two different Lomax distributions using the Probability Density Functions.