Insertion in Red-Black Tree using Python

Red-Black Trees

A red-black tree is a binary search tree with the additional property of being "nearly" adjusted. Every node in a red-black tree has a color, either red or black, and these colors are utilized to keep up with balance during insertions and deletions.

Red-Black Tree Insertion Algorithm:

Begin at the 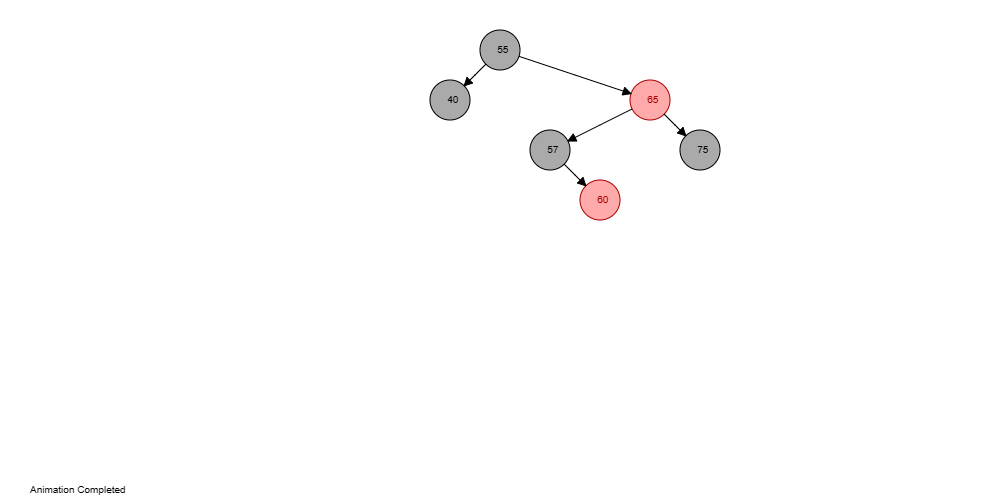root of the tree.
Traverse the tree descending, following the binary search tree property, to track down the suitable area for the new node insertion.
Embed the new node as a red leaf node.
Fix any infringement of the red-black tree properties that might have been presented by the insertion utilizing a bunch of rotation and recoloring tasks.

Code

# Python code for Red-Black Tree
class Node:
    def __init__(self, key, color='R'):
        self.key = key
        self.color = color
        self.left = None
        self.Right = None
        self.parent = None

class RedBlackTree:
    def __init__(self):
        self.TNULL = Node(None)
        self.root = self.TNULL

    def left_rotate(self, x):
        y = x.right
        x.right = y.left
        if y.left != self.TNULL:
            y.left.parent = x
        y.parent = x.parent
        if x.parent is None:
            self.root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y
        y.left = x
        x.parent = y

    def right_rotate(self, y):
        x = y.left
        y.left = x.right
        if x.right != self.TNULL:
            x.right.parent = y
        x.parent = y.parent
        if y.parent is None:
            self.root = x
        elif y == y.parent.left:
            y.parent.left = x
        else:
            y.parent.right = x
        x.right = y
        y.parent = x

    def insert(self, key):
        new_node = Node(key)
        new_node.parent = None
        new_node.key = key
        new_node.left = self.TNULL
        new_node.right = self.TNULL
        new_node.color = 'R'

        y = None
        x = self.root

        while x != self.TNULL:
            y = x
            if new_node.key < x.key:
                x = x.left
            else:
                x = x.right

        new_node.parent = y

        if y is None:
            self.root = new_node
        elif new_node.key < y.key:
            y.left = new_node
        else:
            y.right = new_node

        if new_node.parent is None:
            new_node.color = 'B'
            return

        if new_node.parent.parent is None:
            return

        self.insert_fix(new_node)
    def insert_fix(self, k):
        while k.parent.color == 'R':
            if k.parent == k.parent.parent.right:
                u = k.parent.parent.left
                if u.color == 'R':
                    u.color = 'B'
                    k.parent.color = 'B'
                    k.parent.parent.color = 'R'
                    k = k.parent.parent
                else:
                    if k == k.parent.left:
                        k = k.parent
                        self.right_rotate(k)
                    k.parent.color = 'B'
                    k.parent.parent.color = 'R'
                    self.left_rotate(k.parent.parent)
            else:
                # Similar case for the right side
                pass
        self.root.color = 'B'
# Example usage
rb_tree = RedBlackTree()
rb_tree.insert(55)
rb_tree.insert(40)
rb_tree.insert(65)
rb_tree.insert(60)
rb_tree.insert(75)
rb_tree.insert(57)

Output:

Insertion:

BST Insertion:

Begin by inserting the new node as you would in a standard binary search tree (BST). Place the node in a suitable position in light of the examination of key qualities. Variety the Node-Red: Upon insertion, variety the recently inserted node as red. This may at first disregard a few properties of the red-black tree.

Fix Violations (Insert Fix):

To guarantee that the tree keeps up with the red-black properties, you want to play out a progression of recoloring and rotation tasks known as the "insert fix." This fix reestablishes the equilibrium and properties of the tree while obliging the new red node.

Check assuming that the parent of the recently inserted node is likewise red. If it is, there's a possible violation of the red property.
On the off chance that the parent's uncle is red, recolor the parent and uncle as black, and the grandparent as red. This keeps up with the black property along the way and helps in reestablishing the red property.
On the off chance that the parent's kin is black or invalid, perform rotations and recoloring to reestablish harmony. Contingent upon whether the recently inserted node is the left child of its parent and the parent is the right child of its parent (as well as the other way around), perform proper rotations and recoloring.
Rehash these means if vital, climbing the tree until all properties are reestablished.

Balancing the Tree: Recoloring and Rotation

Double Red:

When both the parent and uncle of the recently embedded node are red, recolor the parent and uncle to dark and the grandparent to red. This guarantees that the red property is reestablished. The cycle might go on up the tree to fix further lopsided characteristics.

Misalignment:

When the recently embedded node is the left child of a right child (or the other way around), rotations are performed to realign the tree. This keeps up with the dark property and guarantees balance.

Next TopicPython Code for Red-Black Tree

← prev next →