Forward Chaining and backward chaining in AIIn artificial intelligence, forward and backward chaining is one of the important topics, but before understanding forward and backward chaining lets first understand that from where these two terms came. Inference engine:The inference engine is the component of the intelligent system in artificial intelligence, which applies logical rules to the knowledge base to infer new information from known facts. The first inference engine was part of the expert system. Inference engine commonly proceeds in two modes, which are:
Horn Clause and Definite clause: Horn clause and definite clause are the forms of sentences, which enables knowledge base to use a more restricted and efficient inference algorithm. Logical inference algorithms use forward and backward chaining approaches, which require KB in the form of the first-order definite clause. Definite clause: A clause which is a disjunction of literals with exactly one positive literal is known as a definite clause or strict horn clause. Horn clause: A clause which is a disjunction of literals with at most one positive literal is known as horn clause. Hence all the definite clauses are horn clauses. Example: (¬ p V ¬ q V k). It has only one positive literal k. It is equivalent to p ∧ q → k.A. Forward ChainingForward chaining is also known as a forward deduction or forward reasoning method when using an inference engine. Forward chaining is a form of reasoning which start with atomic sentences in the knowledge base and applies inference rules (Modus Ponens) in the forward direction to extract more data until a goal is reached. The Forward-chaining algorithm starts from known facts, triggers all rules whose premises are satisfied, and add their conclusion to the known facts. This process repeats until the problem is solved. Properties of Forward-Chaining:
Consider the following famous example which we will use in both approaches: Example:"As per the law, it is a crime for an American to sell weapons to hostile nations. Country A, an enemy of America, has some missiles, and all the missiles were sold to it by Robert, who is an American citizen." Prove that "Robert is criminal." To solve the above problem, first, we will convert all the above facts into first-order definite clauses, and then we will use a forward-chaining algorithm to reach the goal. Facts Conversion into FOL:
Forward chaining proof:Step-1: In the first step we will start with the known facts and will choose the sentences which do not have implications, such as: American(Robert), Enemy(A, America), Owns(A, T1), and Missile(T1). All these facts will be represented as below.  Step-2: At the second step, we will see those facts which infer from available facts and with satisfied premises. Rule-(1) does not satisfy premises, so it will not be added in the first iteration. Rule-(2) and (3) are already added. Rule-(4) satisfy with the substitution {p/T1}, so Sells (Robert, T1, A) is added, which infers from the conjunction of Rule (2) and (3). Rule-(6) is satisfied with the substitution(p/A), so Hostile(A) is added and which infers from Rule-(7). 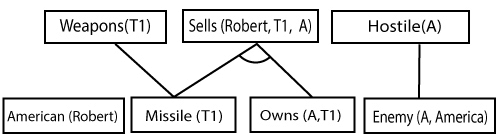 Step-3: At step-3, as we can check Rule-(1) is satisfied with the substitution {p/Robert, q/T1, r/A}, so we can add Criminal(Robert) which infers all the available facts. And hence we reached our goal statement. 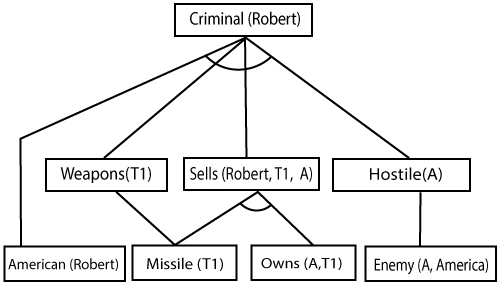 Hence it is proved that Robert is Criminal using forward chaining approach. B. Backward Chaining:Backward-chaining is also known as a backward deduction or backward reasoning method when using an inference engine. A backward chaining algorithm is a form of reasoning, which starts with the goal and works backward, chaining through rules to find known facts that support the goal. Properties of backward chaining:
Example:In backward-chaining, we will use the same above example, and will rewrite all the rules.
Backward-Chaining proof:In Backward chaining, we will start with our goal predicate, which is Criminal(Robert), and then infer further rules. Step-1: At the first step, we will take the goal fact. And from the goal fact, we will infer other facts, and at last, we will prove those facts true. So our goal fact is "Robert is Criminal," so following is the predicate of it.  Step-2: At the second step, we will infer other facts form goal fact which satisfies the rules. So as we can see in Rule-1, the goal predicate Criminal (Robert) is present with substitution {Robert/P}. So we will add all the conjunctive facts below the first level and will replace p with Robert. Here we can see American (Robert) is a fact, so it is proved here. 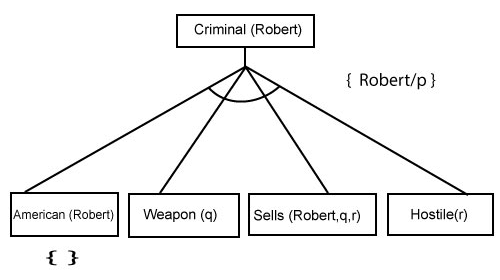 Step-3:t At step-3, we will extract further fact Missile(q) which infer from Weapon(q), as it satisfies Rule-(5). Weapon (q) is also true with the substitution of a constant T1 at q. 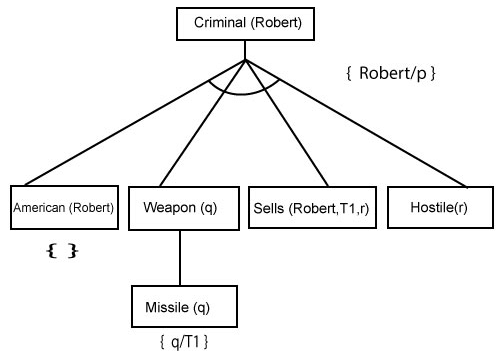 Step-4: At step-4, we can infer facts Missile(T1) and Owns(A, T1) form Sells(Robert, T1, r) which satisfies the Rule- 4, with the substitution of A in place of r. So these two statements are proved here. 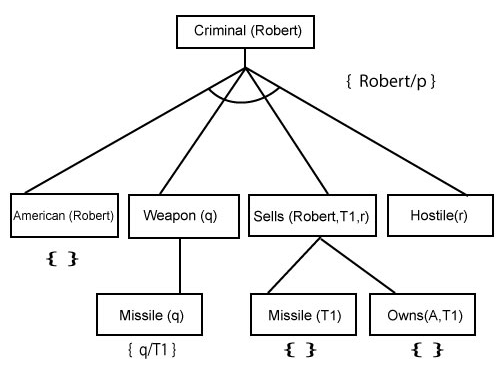 Step-5: At step-5, we can infer the fact Enemy(A, America) from Hostile(A) which satisfies Rule- 6. And hence all the statements are proved true using backward chaining. 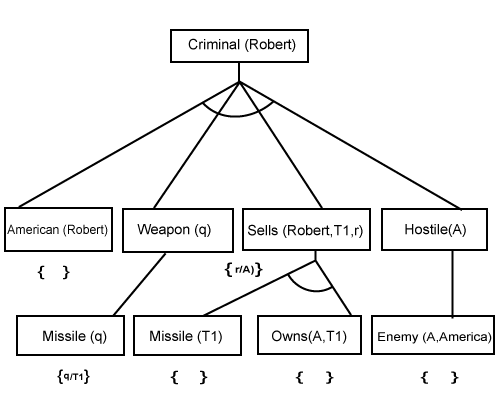 Next Topicbackward chaining vs forward chaining |
We provides tutorials and interview questions of all technology like java tutorial, android, java frameworks
G-13, 2nd Floor, Sec-3, Noida, UP, 201301, India
Home
Python
Java
JavaScript
HTML
SQL
PHP
C#
C++
DS
Aptitude
Reasoning
Selenium
DBMS
C
Andriod
Interview Q