Cross-Validation in SklearnData scientists can benefit from cross-validation while working with machine learning models in two key aspects: it can assist in minimizing the amount of data needed and ensuring the machine learning model is reliable. Cross-validation accomplishes that at the expense of resource use; thus, it's critical to comprehend how it operates before deciding to use it. In this article, we'll quickly go over the advantages of cross-validation, and then we will go through its application using a wide range of techniques from the well-known Python Scikit-learn package. What is Cross-validation?A fundamental error is training the model to make a prediction function and then using the same data to test the model and get a validation score. A model that simply repeats the labels of the samples it has just examined would receive a perfect score but be unable to make predictions about data that has not yet been seen. Overfitting is the term used to describe this circumstance. To avoid this, it is customary to reserve a portion of the given data as a test set (X test, y test) when conducting a (supervised) machine learning study. Because machine learning sometimes begins as an experiment in business contexts, we should note that the word "experiment" does not just refer to academic application. How does Cross Validation Solve the Problem of Overfitting?We create numerous micro train-test splits during cross-validation using our initial training dataset. To fine-tune our model, use these splits. For instance, we divide the dataset into k subgroups for the usual k-fold cross-validation. The remaining dataset is then used as the test dataset after the model has been successively trained on the k-1 dataset. We may test the model on a new dataset in this manner. We will learn about the seven most popular cross-validation approaches in this tutorial. The code samples for each method are also included. The train test split function in scikit-learn can be used to swiftly generate a randomized split into the train and test datasets. To train a linear regression model on the iris dataset, we will import the dataset first. Code Output: (150, 4) (150,) (90, 4) (90,) (60, 4) (60,) 0.888564580463006 There is still a chance of overfitting the test dataset when comparing various settings for estimators. This is why We can adjust the parameters until the estimator works at its best. The model may "leak" information about the test dataset in this method, and evaluation measures may no longer reflect generalization performance. We can resolve this issue by holding out a different portion of the dataset as a "validation set": training is conducted on the training dataset, followed by evaluation on the validation dataset, and when it appears that the experiment has succeeded, we can perform a final assessment on the test set. Data Size ReductionUsually, the data is divided into three sets. Training: used to hone the hyperparameters of the machine learning model and train the model. Testing: used to ensure that the improved model performs well when applied to new data and that the model generalizes correctly. Validation: We execute the last check on utterly unreliable data because, when optimizing, some knowledge about the test dataset seeps into the model due to the choice of parameters. Because we can train and test using the same dataset, adding cross-validation to the workflow helps you eliminate the requirement for the validation dataset. Robust ProcessEven though sklearn's train test split method uses a stratified split, which ensures that the target variable's distribution is the same in both the train and test sets, it's still possible to unintentionally train on a subset that doesn't accurately represent the real world. Methods of Cross-Validation with SklearnHoldOut Cross Validation or Train-Test SplitThis cross-validation procedure randomly divides the entire dataset into a training dataset and a validation dataset. Generally, approximately 70% of the whole dataset is utilized as a training set, and the leftover 30% is taken as a validation dataset. The advantage of this method is that we only need to divide the dataset into the training and validation sets once. The machine learning model will only need to be trained once based on the training dataset, allowing for quick execution. This method is not appropriate for an unbalanced dataset. Consider an unbalanced dataset with classes "0" and "1". Let's assume that 80% of the data falls under class '0' and the rest 20% falls under class '1' upon performing a train-test splitting, with the training dataset making up to 80% of the dataset and the test data making up 20%. The training dataset may contain 100% of the class "0" data, and the test dataset has 100% of the class "1" data. Since our model has never previously encountered class "1" data, it will not generalize well to our testing data. Code Output: Size of Dataset is: 150 Accuracy score for the training dataset is: 0.9904761904761905 Accuracy score for the testing dataset is: 0.9111111111111111 K-Fold Cross ValidationThe entire dataset is divided into K equal-sized pieces using the K-Fold cross-validation procedure. Each division is referred to as a "Fold." We refer to it as K-Folds because there are K pieces. The other K-1 folds are utilized as the training dataset, while One of the Fold is employed as a validation dataset. Until each fold is employed as a validation dataset and the leftover folds are the training datasets, the procedure is repeated K times. The average accuracy of the k number of models of the validation dataset is used to calculate the model's final accuracy. Code Output: Size of Dataset is: 150 K-fold Cross Validation Scores are: [1. 1. 0.86666667 0.93333333 0.83333333] Mean Cross Validation score is: 0.9266666666666665 This technique should not evaluate unbalanced datasets. All the folds of the training dataset may only contain samples from class "0" and not any samples from class "1," as was mentioned in the context of HoldOut cross-validation. And validation dataset will include a sample having class "1". Additionally, we cannot use time series data with this-the ordering of the samples matters for Time Series data. As opposed to this, samples are chosen at random for K-Fold Cross-Validation. Stratified K-Fold Cross ValidationThe improved K-Fold cross-validation method known as stratified K-Fold is typically applied to unbalanced datasets. The entire dataset is split into K-folds of the same size, just like K-fold. However, in this method, each fold will contain the same proportion of target variable occurrences as the entire dataset. This method performs correctly with unbalanced data. In stratified cross-validation, each fold will represent all data classes in the same proportion across the entire dataset. The ordering of the samples matters for time series data; hence this method is not appropriate for time series. Stratified Cross-Validation, however, chooses samples in random order. Code Output: Size of Dataset is: 150 Stratified k-fold Cross Validation Scores are: [0.96666667 1. 0.93333333 0.96666667 1. ] Average Cross Validation score is: 0.9733333333333334 Leave P Out Cross ValidationA thorough cross-validation method called LeavePOut cross-validation uses the n-p samples for training the model and the leftover p-samples as the validation dataset. Assume that the dataset contains 100 samples. If we choose p=10, 10 data entries will be utilized as the validation dataset for each iteration, while the rest 90 samples will constitute the training dataset. This procedure is repeatedly executed until the entire dataset has been split into an n-p training sample dataset and a validation dataset of p-samples. Every data sample is utilized for training and validation. High computing time is required by this method. The method mentioned above will take more time to compute because it will keep executing itself until all samples have been used as a validation dataset. This approach is not appropriate for unbalanced datasets. Similar to K-Fold Cross-validation, our model may not be generalized for the validation dataset if the training dataset contains samples from only one class. Code Output: Size of Dataset is: 150 LeavePOut Cross Validation Scores are: [1. 1. 1. ... 1. 1. 1.] Average Cross Validation score is: 0.9494854586129754 Leave One Out Cross ValidationThis exhaustive cross-validation method, known as "LeaveOneOut cross-validation", uses the n-1 samples as the training dataset and the remaining 1 sample point as the validation dataset. Assume that the dataset contains 100 samples. Following then, one value will be utilised as a validation dataset for each iteration, while the rest 99 samples will serve as the training dataset. As a result, the procedure is repeated until each sample in the dataset has served as a validation sample. With p=1, it is equivalent to LeavePOut cross-validation. Code Output: Size of Dataset is: 150 LeavePOut Cross Validation Scores are: [1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 0. 0. 1. 1. 1. 0. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1. 1.] Average Cross Validation score is: 0.9466666666666667 Monte Carlo Cross Validation(Shuffle Split)A remarkably versatile cross-validation technique is Monte Carlo cross-validation, often referred to as Shuffle Split cross-validation. The datasets are arbitrarily divided into datasets to train and validate models in this method. We have chosen how many portions of the dataset will serve as a training dataset and which part will serve as a validation dataset. The leftover dataset is not used in the training and validation datasets if the combined percentage of the training and the validation dataset size does not equal 100. Let's assume we have 100 samples, of which 60% will be utilized as training data, and 20% will be used for validating the model. The remaining 20% (100 - (60 + 20)) will not be used. We must specify how many times the splitting must occur.
An issue is that the model might not choose some samples in either the training or validation dataset. Additionally, this method is unsuitable for datasets with imbalances. After the length of the training dataset and the validation, the dataset has been determined; all samples are chosen at random. As a result, it is possible that the training dataset does not contain the same class of data as the dataset for validation, making it impossible for the model to generalize to new data. Code Output: Size of Dataset is: 150 Shuffle Split Cross Validation Scores are: [0.93333333 0.91111111 0.91111111 0.93333333 1. 0.97777778 0.93333333 0.93333333 0.95555556 0.93333333] Mean Cross Validation score is: 0.9422222222222223 Time Series Cross ValidationWhat is a Time Series Data? Data collected over a time period in a series is referred to as a time series. There is a chance for a correlation within observations because the data points were collected at close intervals. This is an essential time series feature, differentiating it from standard data. We've already stated that time series data cannot be analyzed using earlier techniques. Therefore, we shall now cross-validate time series data. Cross Validation for Time Series Data Since we cannot use future values to predict values for the past, we are unable to select random samples of the time series data to assign them for training or validation datasets. We divided the data into training and validating the model according to time using the "Forward chaining" approach, also known as rolling cross-validation, because the data chronology is crucial for time series-related tasks. For the training dataset, we begin with a small part of the dataset. We make predictions for subsequent data points using that dataset and verify the accuracy. The succeeding training dataset then contains the predicted values, and further samples are predicted. This is one of the best methods for time series. Other types of data cannot be validated using this. In this strategy, the sequence of the dataset is crucial, but in different methods, the algorithm picks random samples for the training or validation dataset. Code Output: TimeSeriesSplit(gap=0, max_train_size=None, n_splits=6, test_size=None) TRAIN: [0 1 2] TEST: [3] TRAIN: [0 1 2 3] TEST: [4] TRAIN: [0 1 2 3 4] TEST: [5] TRAIN: [0 1 2 3 4 5] TEST: [6] TRAIN: [0 1 2 3 4 5 6] TEST: [7] TRAIN: [0 1 2 3 4 5 6 7] TEST: [8] TimeSeriesSplit Cross Validation Scores are: [0.0, 0.0, 1.0, 0.0, 0.0, 1.0] Comparison of Cross-validation to Train/Test SplitTest/training split: A ratio of 70:30, 80:20, etc., is used to divide the input dataset into a training dataset and test dataset portions. One of its main drawbacks is the considerable variance it offers. Training Data: The dependent feature is known, and the training dataset is utilized for training our model. Test Data: The model, which has already been trained, makes predictions using the test dataset. Although not a component, this has similar characteristics to the training dataset. By dividing our dataset into sets of train/test splits and averaging the results, the cross-validation dataset is utilized to address the drawback of the train/test split. It can be employed if we wish to improve the performance of our model after it has been trained using the training dataset. Since every data point is used for training and testing the model, it is more effective than a train/test split. Limitations of Cross-ValidationThe cross-validation method has some drawbacks, some of which are listed below: It delivers the best results under the best circumstances. However, the contradictory data could lead to a dramatic outcome. There is uncertainty over the type of data used in machine learning, which is one of the significant drawbacks of cross-validation. Because data in predictive modelling changes over time, there may be variations between the training and validation datasets. For instance, if we develop a stock market value prediction model and the dataset is trained on the stock prices from the previous five years. Still, the plausible future stock prices for the following five years could be very different. It is challenging to anticipate the appropriate result in such circumstances. Applications of Cross-Validation
Visualizing Cross Validation MethodsCode Output: 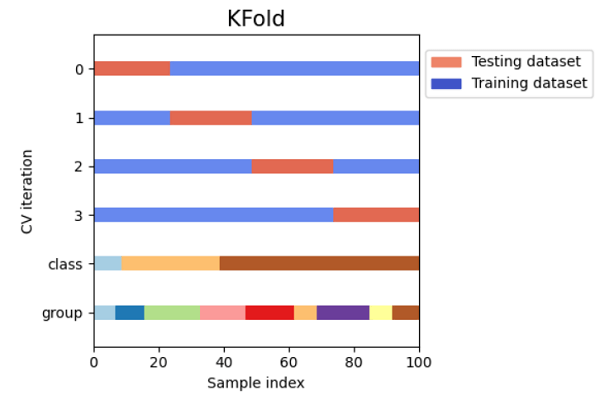 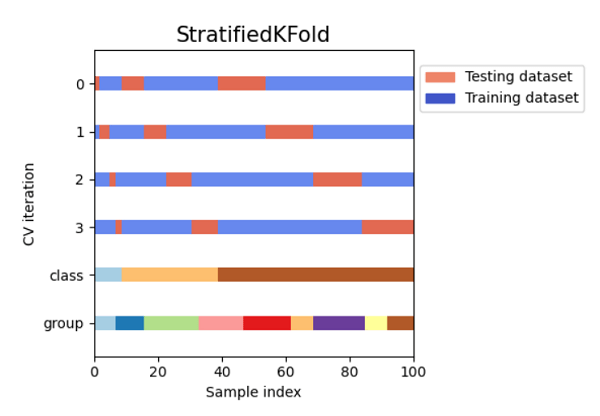 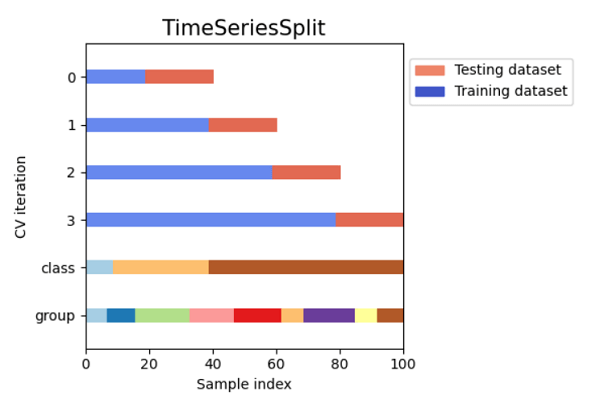 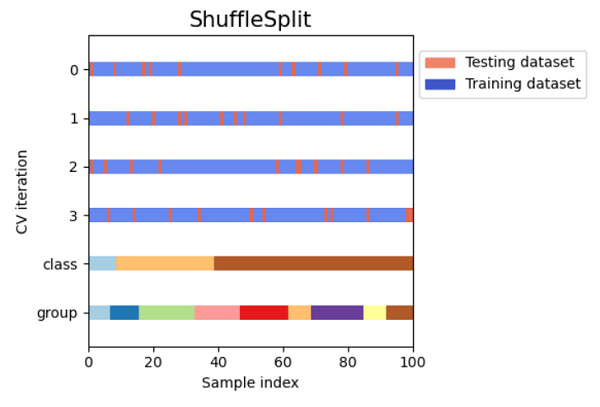 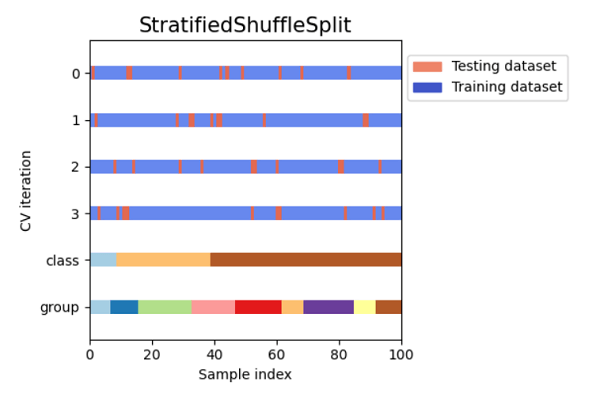 ConclusionMany machine learning tasks use the train-test split basic idea; however, if we have enough resources available to us, we should think about using cross-validation to solve our problem. An inconsistent score throughout the many folds would indicate that we are missing a crucial relationship inside the data we have. This approach also helps us in using fewer data. |