Adaptive Resonance Theory

The Adaptive Resonance Theory (ART) was incorporated as a hypothesis for human cognitive data handling. The hypothesis has prompted neural models for pattern recognition and unsupervised learning. ART system has been utilized to clarify different types of cognitive and brain data.

The Adaptive Resonance Theory addresses the stability-plasticity(stability can be defined as the nature of memorizing the learning and plasticity refers to the fact that they are flexible to gain new information) dilemma of a system that asks how learning can proceed in response to huge input patterns and simultaneously not to lose the stability for irrelevant patterns. Other than that, the stability-elasticity dilemma is concerned about how a system can adapt new data while keeping what was learned before. For such a task, a feedback mechanism is included among the ART neural network layers. In this neural network, the data in the form of processing elements output reflects back and ahead among layers. If an appropriate pattern is build-up, the resonance is reached, then adaption can occur during this period.

It can be defined as the formal analysis of how to overcome the learning instability accomplished by a competitive learning model, let to the presentation of an expended hypothesis, called adaptive resonance theory (ART). This formal investigation indicated that a specific type of top-down learned feedback and matching mechanism could significantly overcome the instability issue. It was understood that top-down attentional mechanisms, which had prior been found through an investigation of connections among cognitive and reinforcement mechanisms, had similar characteristics as these code-stabilizing mechanisms. In other words, once it was perceived how to solve the instability issue formally, it also turned out to be certain that one did not need to develop any quantitatively new mechanism to do so. One only needed to make sure to incorporate previously discovered attentional mechanisms. These additional mechanisms empower code learning to self- stabilize in response to an essentially arbitrary input system. Grossberg presented the basic principles of the adaptive resonance theory. A category of ART called ART1 has been described as an arrangement of ordinary differential equations by carpenter and Grossberg. These theorems can predict both the order of search as the function of the learning history of the system and the input patterns.

ART1 is an unsupervised learning model primarily designed for recognizing binary patterns. It comprises an attentional subsystem, an orienting subsystem, a vigilance parameter, and a reset module, as given in the figure given below. The vigilance parameter has a huge effect on the system. High vigilance produces higher detailed memories. The ART1 attentional comprises of two competitive networks, comparison field layer L1 and the recognition field layer L2, two control gains, Gain1 and Gain2, and two short-term memory (STM) stages S1 and S2. Long term memory (LTM) follows somewhere in the range of S1 and S2 multiply the signal in these pathways.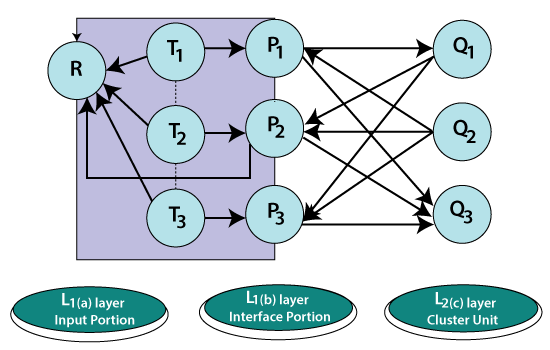

Gains control empowers L1 and L2 to recognize the current stages of the running cycle. STM reset wave prevents active L2 cells when mismatches between bottom-up and top-down signals happen at L1. The comparison layer gets the binary external input passing it to the recognition layer liable for coordinating it to a classification category. This outcome is given back to the comparison layer to find out when the category coordinates the input vector. If there is a match, then a new input vector is read, and the cycle begins once again. If there is a mismatch, then the orienting system is in charge of preventing the previous category from getting a new category match in the recognition layer. The given two gains control the activity of the recognition and the comparison layer, respectively. The reset wave specifically and enduringly prevents active L2 cell until the current is stopped. The offset of the input pattern ends its processing L1 and triggers the offset of Gain2. Gain2 offset causes consistent decay of STM at L2 and thereby prepares L2 to encode the next input pattern without bais.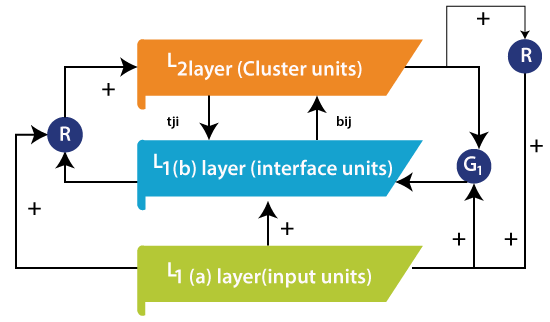

ART1 Implementation process:

ART1 is a self-organizing neural network having input and output neurons mutually couple using bottom-up and top-down adaptive weights that perform recognition. To start our methodology, the system is first trained as per the adaptive resonance theory by inputting reference pattern data under the type of 5*5 matrix into the neurons for clustering within the output neurons. Next, the maximum number of nodes in L2 is defined following by the vigilance parameter. The inputted pattern enrolled itself as short term memory activity over a field of nodes L1. Combining and separating pathways from L1 to coding field L2, each weighted by an adaptive long-term memory track, transform into a net signal vector T. Internal competitive dynamics at L2 further transform T, creating a compressed code or content addressable memory. With strong competition, activation is concentrated at the L2 node that gets the maximal L1 → L2 signal. The primary objective of this work is divided into four phases as follows Comparision, recognition, search, and learning.

Advantage of adaptive learning theory(ART):

It can be coordinated and utilized with different techniques to give more precise outcomes.

It doesn't ensure stability in forming clusters.

It can be used in different fields such as face recognition, embedded system, and robotics, target recognition, medical diagnosis, signature verification, etc.

It shows stability and is not disturbed by a wide range of inputs provided to inputs.

It has got benefits over competitive learning. The competitive learning cant include new clusters when considered necessary.

Application of ART:

ART stands for Adaptive Resonance Theory. ART neural networks used for fast, stable learning and prediction have been applied in different areas. The application incorporates target recognition, face recognition, medical diagnosis, signature verification, mobile control robot.

Target recognition:

Fuzzy ARTMAP neural network can be used for automatic classification of targets depend on their radar range profiles. Tests on synthetic data show the fuzzy ARTMAP can result in substantial savings in memory requirements when related to k nearest neighbor(kNN) classifiers. The utilization of multiwavelength profiles mainly improves the performance of both kinds of classifiers.

Medical diagnosis:

Medical databases present huge numbers of challenges found in general information management settings where speed, use, efficiency, and accuracy are the prime concerns. A direct objective of improved computer-assisted medicine is to help to deliver intensive care in situations that may be less than ideal. Working with these issues has stimulated several ART architecture developments, including ARTMAP-IC.

Signature verification:

Automatic signature verification is a well known and active area of research with various applications such as bank check confirmation, ATM access, etc. the training of the network is finished using ART1 that uses global features as input vector and the verification and recognition phase uses a two-step process. In the initial step, the input vector is coordinated with the stored reference vector, which was used as a training set, and in the second step, cluster formation takes place.

Mobile control robot:

Nowadays, we perceive a wide range of robotic devices. It is still a field of research in their program part, called artificial intelligence. The human brain is an interesting subject as a model for such an intelligent system. Inspired by the structure of the human brain, an artificial neural emerges. Similar to the brain, the artificial neural network contains numerous simple computational units, neurons that are interconnected mutually to allow the transfer of the signal from the neurons to neurons. Artificial neural networks are used to solve different issues with good outcomes compared to other decision algorithms.