Advection Diffusion Equation using Python

Introduction:

The advection-diffusion equation is a central idea in physics and design, with applications spreading over a scope of fields from fluid dynamics to heat movement. The domain of physics and designing is enhanced by the perplexing transaction of advection, diffusion, and the variety of limit conditions that oversee the movement of amounts inside mediums. In this article, we will dive into the mathematical formulation of the advection-diffusion equation, grasp its key parts - advection, and diffusion, investigate limit conditions, and carry out it utilizing Python. We will additionally saddle the force of Python to carry out these ideas, offering an involved understanding of their true applications. Toward the finish of this article, you will have a complete understanding of this equation and how to recreate its conduct utilizing Python libraries like NumPy and Matplotlib.

Advection and Diffusion:

Advection addresses the mass transport of an amount, like heat or concentration, because of the medium's fluid velocity. This prompts the quick movement of amounts over distances. In actuality, diffusion, driven by the irregular movement of particles, makes the amount scatter slowly after some time. Advection pushes change through movement, while diffusion cultivates steady conveyance, frequently checking advection.

Mathematical Formula :

The advection-diffusion equation depicts the transport of an amount, like a synthetic concentration or temperature, in a medium exposed to both advection (mass movement) and diffusion (irregular sub-atomic movement). Mathematically, the 1D advection-diffusion equation is communicated as:

Where:

• c addresses the concentration or amount being transported.
• t means time.
• x implies the spatial direction.
• u is the advection velocity.
• D is the diffusion coefficient.

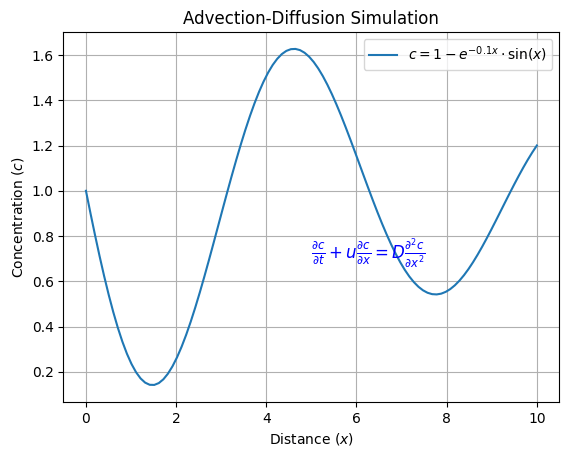Understanding Advection and Diffusion:

Advection addresses the mass movement of the amount because of the fluid's velocity u. This can prompt concentration changes as the fluid streams. Then again, diffusion results from irregular atomic movement, making the amount spread out over the long haul, independent of the fluid's movement.

Advection:

Transport Phenomenon: Advection involves the mass movement of a substance within a fluid medium. It happens when the actual fluid is moving, carrying the substance alongside it.

Convection Currents: Advection brings about convection currents, where locales of higher concentration are transported to districts of lower concentration, leading to mixing and changes in the substance's appropriation.

Dominant in Flow: In situations with fast fluid movement, like wind, sea currents, and flow in pipelines, advection turns into the dominant component affecting the substance's transport.

Engineering Applications: Advection assumes a huge part in natural examinations, including air contamination scattering modeling, as well as in the plan of heat exchangers and cooling frameworks.

Mathematical Expression: Mathematically, advection is addressed by the initial term in the advection-diffusion equation, where the adjustment of substance concentration regarding time is corresponding to its velocity duplicated by the spatial concentration gradient.

Diffusion:

Random Molecular Movement: Diffusion happens because of the random movement of particles. It prompts the steady scattering of a substance from districts of higher concentration to locales of lower concentration.

Equilibrium Attainment: Over the long haul, diffusion will in general balance the concentration all through the medium, resulting in a condition of equilibrium where no net movement happens.

Role in Biology: Diffusion is fundamental in natural cycles like supplement trade among cells and the movement of gases across cell films.

Influence of Temperature: Diffusion rates are influenced by temperature; higher temperatures speed up molecular movement and increase the pace of diffusion.

Mathematical Expression: In the advection-diffusion equation, diffusion is portrayed continuously term, where the adjustment of concentration is relative to the diffusion coefficient duplicated by the spatial second subsidiary of the concentration.

Python Implementation

Python, a flexible language, engages us to emerge these ideas. With the NumPy and Matplotlib libraries, we can productively reenact advection and diffusion situations. We should consider a basic model using finite contrasts.

Code

Output: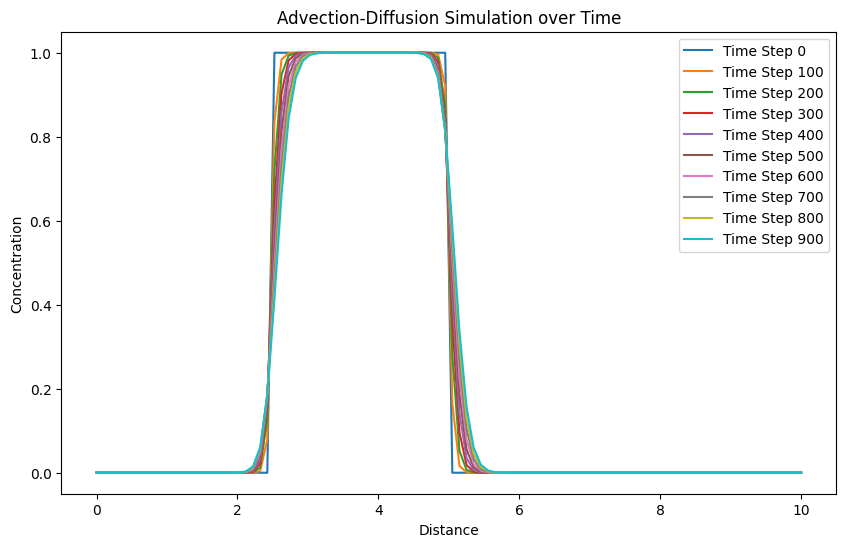

Explanation:

1. The spatial distance inside the domain is represented by the plot's horizontal x-axis. The x-axis is segmented into distinct spatial locations, and the domain length is set to 10 units.
2. The concentration of the chemical being conveyed is shown on the vertical y-axis. The scaled concentration numbers represent the relative concentration of the chemical at various locations throughout space and are based on the simulation.
3. The graphic shows several curves, each of which represents a different time step. The curves depict the evolution of the concentration profile over time.
4. The time interval where the concentration profiles were collected is indicated by the labels on the curves. The labels span the whole simulation period and are uniformly spaced.
5. You can see the concentration profile change over time as you travel down the x-axis from left to right. Changes in the spread and form of the concentration curve reveal the substance's advective and diffusional movement.
6. The concentration profile may not vary much at first, suggesting that diffusion is dominant. As the simulation goes on, you could notice how advection gradually begins to affect the concentration distribution, resulting in increasingly noticeable changes.
7. The shifting and enlarging of the concentration curves reveal the interplay between advection and diffusion. Advection velocity (u) regions may move and vary in concentration more quickly.
8. You could see that the particular chemical concentration changes over time in the domain by looking at the curves from left to right. This clarifies how advection and diffusion interact with one another and the system as a whole.

Limit Conditions:

To completely settle the advection-diffusion equation, limit conditions are fundamental. These circumstances direct the way that the amount acts at the limits of the space. Normal circumstances incorporate fixed value (Dirichlet), zero-gradient (Neumann), and convective limit conditions.

Dirichlet Condition: A Dirichlet limit condition indicates the value of the amount being transported at the limit. For instance, setting a decent temperature at the limit of a heated plate.

Neumann Condition: Neumann limit conditions authorize no motion at the limit, meaning there's no movement of the substance across the limit.

Convective Condition: Convective limit conditions represent interactions with outer flows. They think about both the amount's diffusion and advection at the limit.

Role in Simulations: Selecting fitting limit conditions is pivotal for exact simulations. Incomplete or incorrect circumstances can prompt ridiculous outcomes.

Dynamic Interactions: In certain situations, limit conditions could change after some time as conditions develop, requiring cautious thought and execution in simulations.

Mathematical Techniques and Python Execution:

Executing the advection-diffusion equation logically can be testing, particularly for complex situations. Mathematical techniques, as limited distinction strategies, act the hero. We should utilize Python to exhibit a basic execution utilizing limited contrasts.

Finite Contrast: Finite distinction techniques surmised subsidiaries using discrete contrasts in existence. They change the continuous equations into a discrete network, reasonable for computational reproduction.

Solidness and Exactness: Choosing fitting time steps and spatial intervals is fundamental for strength and precision. More modest advances upgrade exactness however increase calculation time.

Explicit versus Implicit: Explicit strategies compute future values exclusively founded on current values, while implicit techniques think about future values as questions in the equation framework.

Crank-Nicolson Plan: The Crank-Nicolson plot finds some kind of harmony among explicit and implicit techniques, providing better precision and steadiness for advection-diffusion issues.

Computational Power: Mathematical techniques permit us to reenact intricate situations that need logical arrangements. They influence the computational force of current PCs to display genuine peculiarities.

Conclusion:

The advection-diffusion equation assumes an essential part in understanding the transport peculiarities in different fields. In this article, we covered its mathematical formulation, the jobs of advection and diffusion, limit conditions, and a Python execution utilizing limited contrasts. By executing and picturing the equation's conduct utilizing Python libraries, you've acquired a strong understanding of its importance and reasonable applications. Go ahead and investigate more mind-boggling situations and refine your mathematical strategies to recreate genuine situations precisely.